Encoding Problems
Before we can define mathematical computation models(like Turing machines) that correspond to machines, we need a way to encode these problems.
We can observe that an instance of any problem can always be encoded by a sequence of 0s and 1s. Rather, we can use a combination of symbols to encode a problem.
- The finite set of symbols and characters used for encoding is called the alphabet $\Sigma$. For example, $\Sigma = {0, 1}$.
- A string $w$ over an alphabet $\Sigma$ is a finite sequence of those symbols.
- $\Sigma^*$ Represents the set of all strings over $\Sigma$.
- A language represents a particular set of strings over an alphabet.
Operations Over Strings
Many operations can be performed on strings to modify them:
- Given strings $u$ and $v$, $u.v$ denotes their concatenation.
- A string $u$ is a prefix of string $w$ if there exists a string $v$ such that $w = u.v$.
- A string $u$ is a suffix of string $w$ if there exists a string $v$ such that $w = v.u$.
- A string $u$ is a substring of string $w$ if there exists a string $v$ and $v’$ such that $w = v.u.v’$.
Finite State Automata
Automaton $M$ has a finite number of states. It begins with an initial state, and based on the symbol currently being processed.
Let’s construct an automaton for the language $A = { w$ | $w$ contains an even number of a’s$}$, where $\Sigma = {a, b}$.
Let us define two states, $q_1, q_2$. Start with the initial state, $q_1$. On a given character, if it is $a$, we transition from $q_1 \to q_2$, or $q_2 \to q_1$. Otherwise, we stay in the current state.
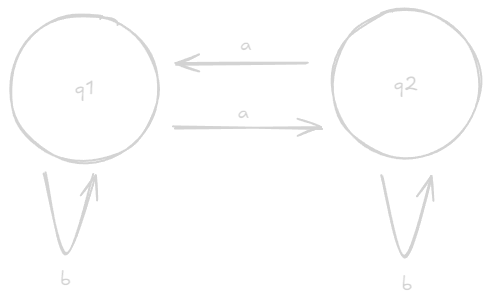
If by the end of the string, we are in state $q_1$, then $w$ has an even number of a’s and belongs in $A$. This type of machine is called a deterministic finite automaton, or DFA.
The transitions of this state is represented by a transition function $\delta$. If $M$ reads the symbol $x$ on current state $y$, then the next state will be $\delta(y, x)$.
A language $A$ is called a regular language if it can be solved by a DFA.