Operations on Regular Languages
Lets take the following two languages:
$A_1 = \{w | \text{ w ends with a}\}$ $A_2 = \{w | \text{ w contains at least one b} \}$
 2024-09-24 19.48.23.excalidraw.png)
 2024-09-24 19.51.35.excalidraw.png)
However, what if I gave the set $A = A_1 \cap A_2$. Is it possible to construct a DFA for $A$ from the DFAs for $A_1$ and $A_2$? Let us call this DFA $M$. What state should $M$ maintain?
In some way, we want to simultaneously execute both $M_1$ and $M_2$ on its input. What if we were to store the state of M as some sort of tuple, like (state of $M_1$, state of $M_2$)? This way, we can essentially simulate two DFAs, where we have a state $(q, s)$, and for a processed letter, we go to the states that each DFA would have individually gone to, giving us $(q’, s’)$.
For the previous DFA, that would look like this:
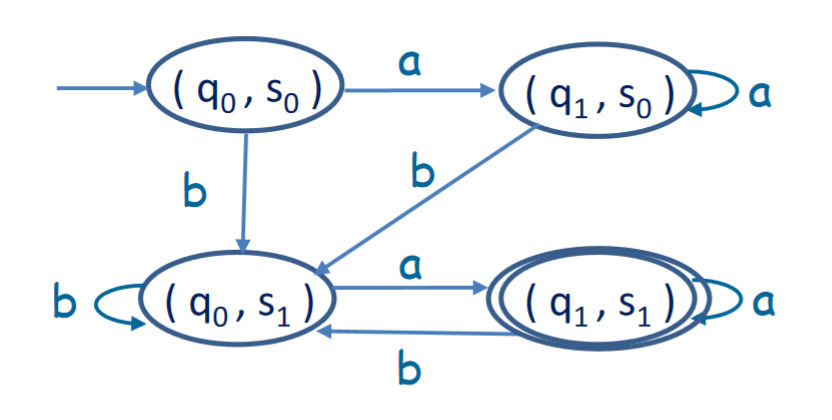
This is the DFA $M$, that accepts a string iff it is accepted by $M_1$ and $M_2$.
Formal Definition
Given two DFAs: $M_1 = (Q_1, \Sigma, q_{01}, F_1, \delta_1)$ $M_2 = (Q_2, \Sigma, q_{02}, F_2, \delta_2)$
For $M$ where $L(M) = L(M_1) \cap L(M_2)$, $M$ is defined as the following:
- $Q = Q_1 \times Q_2 = \{(q_1, q_2) | q_1 \in Q_1 \land q_2 \in Q_2\}$
- Note: this is cartesian product
- $q_0 = (q_{01}, q_{02})$
- $\delta((q_1, q_2), \sigma) = (\delta_1(q_1, \sigma), \delta_2(q_2, \sigma))$
- $F = F_1 \times F_2$
This method, however, creates a large number of states. Specifically, it creates the $m_1 \times m_2$ states, where $m_1$ and $m_2$ are the number of states of their respective DFAs. However, it is proven that this is the optimal solution.
Closure Under Intersection
Theorem: The class of regular languages is closed under intersection
Proof: Consider two regular languages $A_1$ and $A_2$. By definition of regular languages, there must exist DFAs $M_1$ and $M_2$ that define the two languages. Using the product construction just defined, we can construct $M$, which will define $A_1 \cap A_2$. This proves that $A_1 \cap A_2$ is regular.
Union
Theorem: The class of regular languages is closed under union
Proof: Consider two regular languages $A_1$ and $A_2$. By definition of regular languages, there must exist DFAs $M_1$ and $M_2$ that define the two languages. Is there a way we can modify the product/intersection construction to create a DFA that works on the union of these two languages?
It is actually very simple to do this. Currently, the above construction simulates both DFAs. However, the set of accepting states for it is only the cartesian product of the set of accepting states for both DFAs. That is to say, $(q, s) \in F$ if and only if $q \in F_1 \land s \in F_2$. If we were to change that to be that the set of accepting states was whether $q \in F_1$ or $s \in F_2$, then this would be a valid DFA for the union of the languages, since a string $w$ is accepting if and only if it is accepted by $M_1$ or $M_2$.
Formal Definition
Given two DFAs: $M_1 = (Q_1, \Sigma, q_{01}, F_1, \delta_1)$ $M_2 = (Q_2, \Sigma, q_{02}, F_2, \delta_2)$
For $M$ where $L(M) = L(M_1) \cap L(M_2)$, $M$ is defined as the following:
- $Q = Q_1 \times Q_2 = \{(q_1, q_2) | q_1 \in Q_1 \land q_2 \in Q_2\}$
- Note: this is cartesian product
- $q_0 = (q_{01}, q_{02})$
- $\delta((q_1, q_2), \sigma) = (\delta_1(q_1, \sigma), \delta_2(q_2, \sigma))$
- $F = (F_1 \times Q_2) \cup (Q_1 \times F_2)$
This also proves the above theorem.
Closure Under Complementation
The complement of a language is simply the set of strings that are not in the language. $\neg A = \{w | w \notin A\}$
If we know $A$ to be regular, then can we conclude $\neg A$ is also regular?
Yes. All we need to do is toggle the role of accepting and rejecting states. If $q$ was an accepting state in $M$, then it is now a rejecting state in $M’$ and vice versa.
Formal Definition
Given two DFAs: $M_1 = (Q_1, \Sigma, q_{01}, F_1, \delta_1)$ $M_2 = (Q_2, \Sigma, q_{02}, F_2, \delta_2)$
For $M$ where $L(M) = L(M_1) \cup L(M_2)$, $M$ is defined as the following:
- $Q = Q_1 \times Q_2 = \{(q_1, q_2) | q_1 \in Q_1 \land q_2 \in Q_2\}$
- Note: this is cartesian product
- $q_0 = (q_{01}, q_{02})$
- $\delta((q_1, q_2), \sigma) = (\delta_1(q_1, \sigma), \delta_2(q_2, \sigma))$
- $F = Q \backslash F$
Language Concatenation
The concatenation of strings $u$ and $v$ is defined as $u.v$. The concatenation of two languages $A$ and $B$ is defined as $A.B = \{u.v | u \in A \land v \in B \}$. That is, a string $w$ is in $A.B$ if it can be split into two (not necessarily equal) strings such that the first part is in $A$ and the second part is in $B$.
Example
- Let $A$ be the set of strings that end with $a$
- Let $B$ be the set of strings containing only $b$
- Then, $A.B$ is the set of strings that has an $a$ that is followed by only $b$
Theorem: The class of regular languages is closed under concatenation
Proof: Consider two regular languages $A_1$ and $A_2$. By definition of regular languages, there must exist DFAs $M_1$ and $M_2$ that define the two languages. We can construct a DFA that defines $M$ where $M = M_1.M_2$
To construct this, however, we need another important concept
NFAs with $\mathcal{E}$-Transitions
An $\mathcal{E}$-Transition is a transition in which the state may change without consuming any input. In the execution tree, this is basically creating two threads without actually consuming a letter. Remember that a string is accepted as long as some execution path succeeds.
Consider the following $\mathcal{E}$-NFA
 2024-09-24 21.33.10.excalidraw.png)
If you try, you can see that this accepts $ab$, but does not accept $ba$.
The transition function now takes the structure of $\Delta : Q \times [\Sigma \cup \{\mathcal{E}\} \to 2^Q$. The empty transitions do not increase expressiveness: an $\mathcal{E}$-NFA can still be compiled into an equivalent DFA just by modifying the subset construction.
Towards Concatenation Construction
Given an input $w$, $M$ needs to check that it is possible to split it into two parts such that each are accepted by $M_1$ and $M_2$ respectively. Intuitively, $M$ should first act like $M_1$, and then when $M_1$ is in a final state, start acting like $M_2$ for the remainder of the string. The challenge comes with when deciding to switch or and try with a different partition of substrings.
However, using an $\mathcal{E}$-NFA, we can get a pretty easy solution to this. When we are a final state for $M_1$, we can simply put a $\mathcal{E}$-transition to the initial state of $M_2$. This way, $M_1$ will continue running on its own thread for the entire string. However, for every substring for which $M_1$ is satisfied, we will be at a final state, so we will start a new thread at the beginning of $M_2$ for the remaining of the string in that instance. This way, we will be able to test every partition for which the first substring is valid under $M_1$.
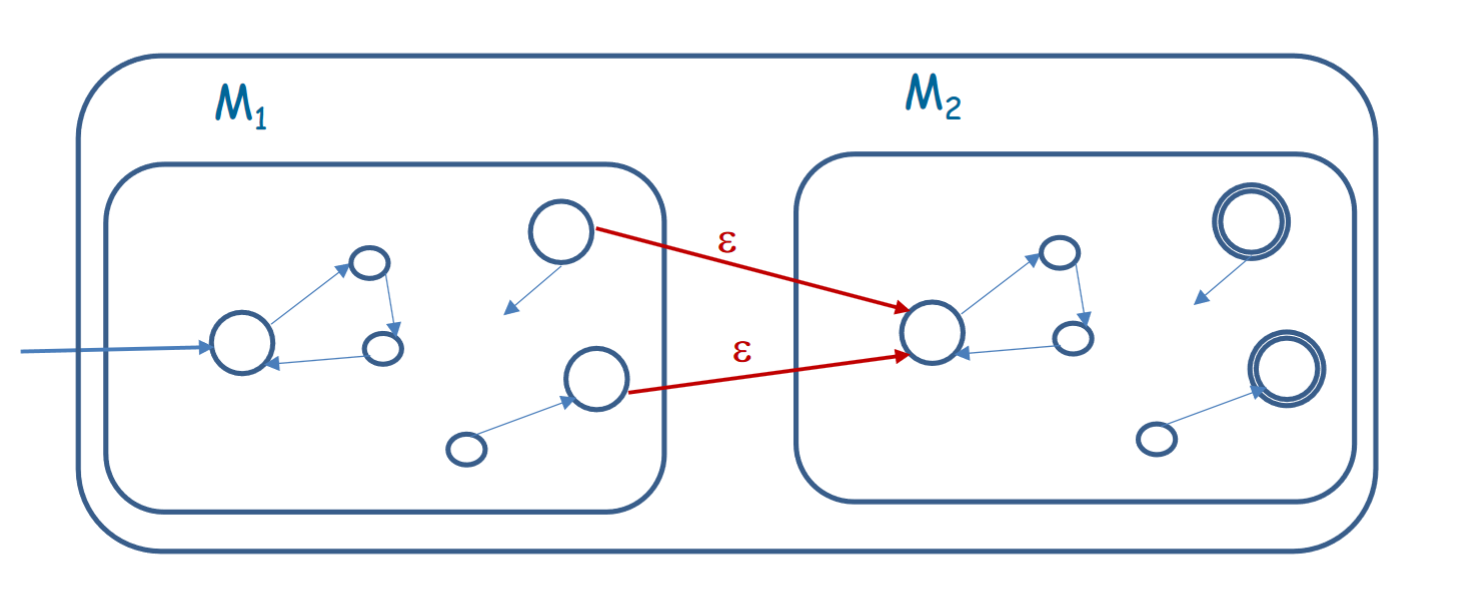
Formal Definition
Given two DFAs: $M_1 = (Q_1, \Sigma, q_{01}, F_1, \delta_1)$ $M_2 = (Q_2, \Sigma, q_{02}, F_2, \delta_2)$
For $M$ where $L(M) = L(M_1).L(M_2)$, $M$ is defined as the following $\mathcal{E}$-NFA:
- $Q = Q_1 \cup Q_2$
- $q_0 = q_{01}$
- $\delta(q, \sigma) = \{\delta_1(q, \sigma)\} \text{ if Q is in } Q_1 \text{ and } \{\delta_2(q, \sigma)\} \text{ otherwise}$
- $\delta(q, \mathcal{E}) = \{q_{02}\} \text{ if q is in } F_1 \text{ and } \{\} \text{ otherwise}$
- $F = F_2$
This also proves the above theorem that regular languages are closed under construction.
Extra Operations
Prefix Operation A string $u$ is defined as a prefix of $w$ if $w = u.v$ for some string $v$. $Prefix(A) = \text{set of all prefixes of all strings of A}$
Theorem: Regular languages are closed under the prefix operation
Shuffle Operation A string $u$ is a shuffle of $w$ if it can be obtained by permuting(shuffling) the characters in $w$. $Shuffle(A) = \text{set of all strings that are a shuffle of strings in } A$
Theorem: Regular languages are not closed under the shuffle operation
To recap, regular languages are closed under union, intersection, complementation, concatenation, prefix, but not shuffle.