Table of Contents
Open Table of Contents
Turing Machines
Let’s take the language $A$ of palindromes, where $\Sigma = {a, b}$. We know that $A$ is not regular, and it follows that there is no DFA for $A$. However, that doesn’t mean we can’t design a machine that solves it. In particular, we can design a turing machine for it.
The components of a turing machine begin with its tape. The tape of a turing machine is an array of cells where each element can hold a symbol from a superset of $\Sigma$, called the tape alphabet. This tape is potentially unbounded on the right, and plays the role of memory in a modern computer. Initially, the tape holds the input string, and has blanks to the right of it once it reaches the end.
Like a DFA, a TM has finitely many states $Q$, one of which is labeled $q_0$. A turing machine also has a head, which is essentially a mobile pointer that points to a tape cell. Initially, the TM is in state $q_0$ and the head points to the left-most tape cell.
Like the DFA, the most important part of the TM are the transitions. A single transition of a TM will have the following structure: based on the current state and symbol read by head, overwrite the current symbol, move the head left/right, and update the state. This way, the machine can go back and forth on the tape, reading and writing cells.
Palindromes
Returning to our palindromes problem, we can think of a pretty simple high level algorithm to figure out whether a string is a palindrome or not:
- If the first symbol is $a$, move all the way to the right to check that the last symbol equals $a$. Do the same for $b$.
- If the check fails, reject the input immediately
- If the check succeeds, move back to the left, and repeat for the next tape cell.
But we need to consider more than just that: When should we stop while moving back to the left? How do we check that two symbols match?
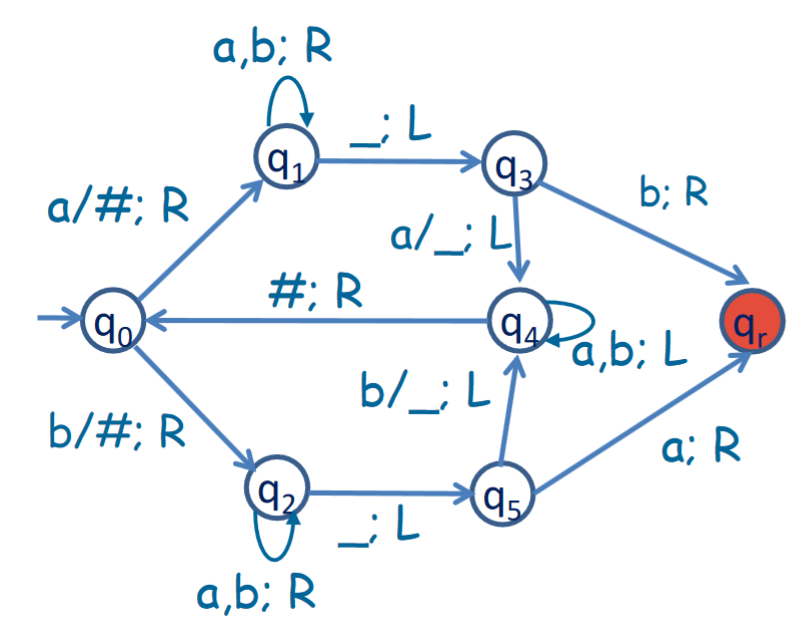
Let us begin at state $q_0$. If the head reads $a$ from here, then we replace it with # and move the head one step to the right, and go to state $q_1$. However, if we read $b$, we go to state $q_2$.
WLOG, let us say we had an $a$. Now, we can skip right until the end of the input, which we know we have reached when we encounter a $\_$, at which point we will move left and to a new state $q_3$. From here, if we read a $b$, then clearly this is not a palindrome, and we want to reject this string. We therefore send it to $q_r$, which is a rejecting state, which will automatically reject the input.
However, if we read an $a$, that means that the palindrome condition is fulfilled up until this point. Therefore, we replace the tape cell with a $\_$ and send it to state $q_4$, which will move left skipping over $a$ and $b$ until it reads a #, at which point it will go back one right.
Here is a drawing of such a TM. Note that the transitions out of $q_2$ are symmetric to the ones we just described, just for $b$ instead of $a$.
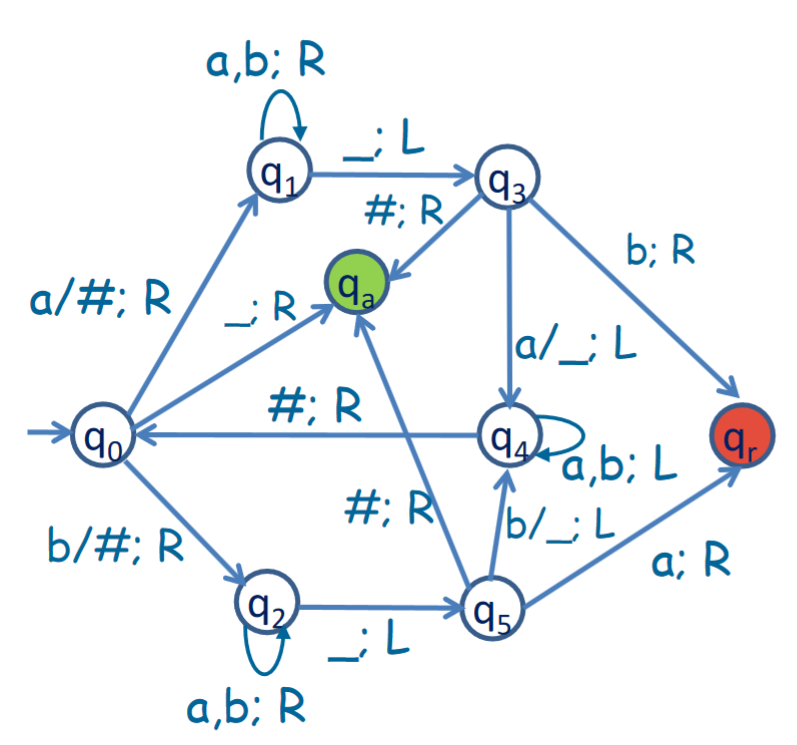
Now, we need to think about what our accepting states are. This is a difficult question. If we do a few examples in our head, we can see that odd length strings and even length strings are treated a bit differently.
If we think about an even length string that is a palindrome, we can see that at the point after we have processed the first half of the characters, we will be left with a tape of the format $(\char35)^n(\char95)^n$. Therefore, we can say that at any point, if we read a $\_$ from state $q_0$, we know it is a palindrome.
Furthermore, thinking about an odd length string, if the string is a palindrome, we will have it confirmed by the point we reach a tape string of the formal $(\char35)^n u (\char95)^n$ where $u$ is some character. Unlike the even length example, $q_0$ will continue processing $u$ as normal. However, we will have set $u$ to # by then. Therefore, after we start moving to the right trying to find a $\char95$, we will reach the $\char95$ immediately to the right, and then jump back left to the # we just created. At this point we will be at state $q_3$ or $q_5$. Therefore, we can say that from either of those states, if we read a #, then we can accept this string as a palindrome.
In a TM, there isn’t necessarily a concept of the end of an input string. Therefore, we instead must send the string here to an accepting state called $q_a$ which, similar to the rejecting state $q_r$, will accept the string immediately.
Turing Machine Components
To recap the turing machine, a turing machine $M$ consists of:
- A finite set $Q$ of states
- Initial state $q_0 \in Q$
- Accepting state $q_a \in Q$
- Rejecting state $q_r \in Q$
- Tape alphabet $\Gamma$
- Input alphabet $\Sigma \subseteq \Gamma$
- Blank symbol $\char95 \in \Gamma, \char95 \notin \Sigma$
- Transition function $\delta : Q \times \Gamma \to Q \times \Gamma \times {L, R}$
- $\delta(q, \sigma) = (q’, \gamma, L/R)$ means that in state $q$, if the current tape cell contains $\sigma$, then write $\gamma$, move L/R, then go to state $q’$